Boostcamp AI Tech (Day 016)
1. 3D 공부
1.1 Lecture 1

CS231A 강의 소개
Computer Vision(컴퓨터 비전) 강좌로, 3D Perception(3D 지각)에서 3D Reconstruction(3D 재구성)까지 다양한 내용을 다루고 있다.
강의 내용 개요
- Introduction: 컴퓨터 비전에 대한 기본 소개 및 강의 개요 설명.
- AI(인공지능)는 현재 기술 발전의 주요 동력으로 작용하고 있으며, Zipline, Waymo, OpenAI’s DALL-E와 같은 다양한 애플리케이션에서 그 활용도를 보여주고 있다.

- 컴퓨터 비전의 주요 분야는 Space/Geometry(공간/기하학), Time/Dynamics(시간/동역학), Semantics(의미론)으로 나눌 수 있다.
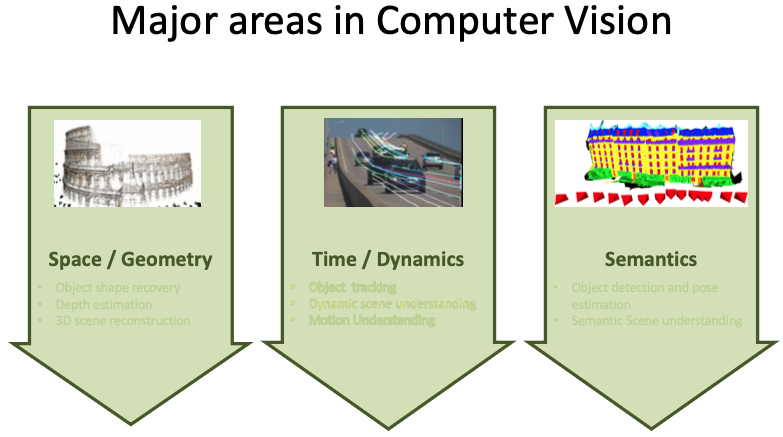
3.1 Space / Geometry
- Object shape recovery

- Depth estimation
- 3D scene reconstruction

3.2 Time / Dynamics, Semantics
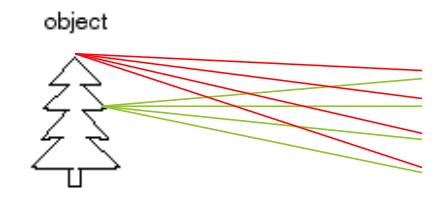
- Object shape recovery
1.2 Lecture 2
Lecture 2: Camera Models 이 강의는 카메라 모델에 대해 다루고 있다. (핀홀 카메라, 렌즈와 카메라의 기하학적 관계 등)
1. Pinhole Cameras
- 핀홀 카메라의 기본 원리와 구성: ** object 앞에 film을 놓아보자! **
 필름을 통해 물체에서 나오는 빛을 직접 받아 이미지를 형성하는 방식이다.
필름을 통해 물체에서 나오는 빛을 직접 받아 이미지를 형성하는 방식이다. - Aperture(조리개)의 역할과 중요성: ** 광선 중 대부분을 차단하는 barrier를 설치하자! ** barrier를 추가해서 대부분의 광선을 차단하면 이미지의 블러가 줄어든다. 이 barrier의 작은 개구 부분을 조리개(aperture)라고 한다. 조리개는 카메라 렌즈의 빛을 텍스트통제하여 이미지를 선명하게 만들어준다.
2. Camera History
- Leonardo da Vinci(레오나르도 다 빈치)가 최초로 기록한 Camera Obscura(카메라 옵스큐라) 개념을 소개
- Johann Zahn(요한 자흔)과 Joseph Nicéphore Niépce(조제프 니세포르 니엡스)가 최초의 휴대용 카메라 및 사진을 개발한 과정
- 사진의 발전과정, Daguerréotypes(다게레오타입) 및 Color Photography(컬러 사진)의 출현
3. Pinhole Perspective Projection
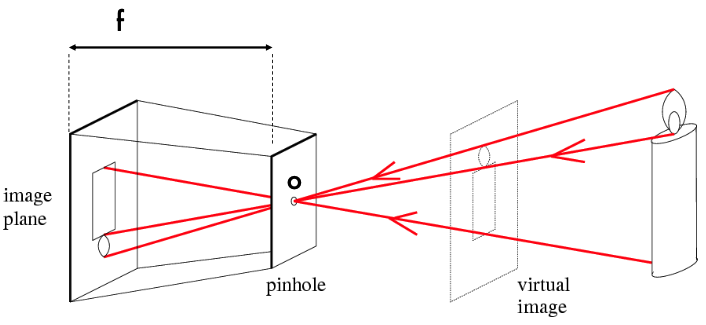 핀홀 카메라는 작은 구멍인 핀홀을 통해 빛이 들어와 이미지가 형성된다.
실제 물체의 각 점에서 나오는 빛이 핀홀을 통과하여 반대 쪽의 이미지 평면에 투영된다.
투영 과정을 통해 3물체가 2D 이미지로 변환된다.
핀홀 카메라는 작은 구멍인 핀홀을 통해 빛이 들어와 이미지가 형성된다.
실제 물체의 각 점에서 나오는 빛이 핀홀을 통과하여 반대 쪽의 이미지 평면에 투영된다.
투영 과정을 통해 3물체가 2D 이미지로 변환된다.
3.1 투영방정식
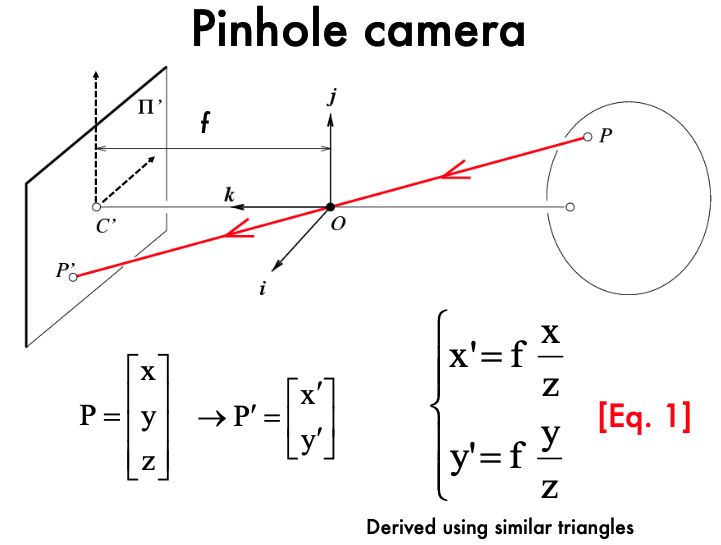 핀홀 카메라에서 이미지 평면에 투영된 점 $(x’, y’)$, 물체의 실제 3D 위치 $(X, Y, Z)$
핀홀 카메라에서 이미지 평면에 투영된 점 $(x’, y’)$, 물체의 실제 3D 위치 $(X, Y, Z)$
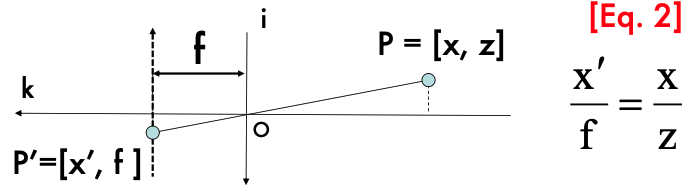
$x’ = \frac{fX}{Z}$ $y’ = \frac{fY}{Z}$ - $f$는 카메라의 초점 거리(focal length) - $Z$는 물체의 깊이(depth) - $(X, Y, Z)$는 물체의 실제 3D 좌표 - $(x’, y’)$는 이미지 평면에서의 2D 좌표
투영 방정식은 3D 공간의 점을 2D 평면으로 변환하는 기하학적 변환이다. 이 변환의 핵심은 원근법(perspective)이다. - 원근법: 물체가 카메라에서 멀어질수록 이미지에서의 크기가 작아지는 현상 - 1. 3D 공간의 점 $(X, Y, Z)$에서 빛이 핀홀을 통과하여 반대쪽 평면에 투영된다. - 2. 이 투영 과정에서, $Z$ 값에 따라 물체의 크기와 위치가 조정된다. - 3. 변환된 2D 좌표 $(x’, y’)$는 실제 이미지로 나타나게 된다.
이미지에서 각 점이 어떻게 계산되고 위치가 정해지는질까? 카메라가 물체에 가까울수록 $Z$ 값이 작아지고, 이는 $(x’, y’)$ 값이 커져 이미지에서 물체가 더 크게 보이는 효과를 준다.
3.2 핀홀 카메라에서 조리개 크기의 중요성
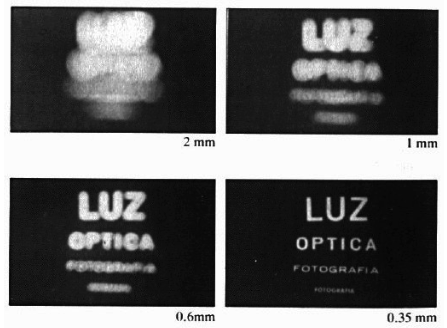
- 핀홀 카메라에서 물체의 빛이 작은 핀홀을 통과하여 필름에 도달한다. 이때 조리개(aperture)의 크기가 이미지의 선명도에 큰 영향을 미친다.
- 조리개 크기가 클 경우, 더 많은 빛이 통과하지만 이미지가 흐릿해진다.
- 조리개 크기가 작을 경우, 빛의 양이 제한되어 선명한 이미지를 얻을 수 있지만, 너무 작으면 충분한 빛이 들어오지 않아 어두운 이미지가 될 수 있다. 렌즈를 추가하면 빛의 양을 조절하고, 이미지를 더 선명하게 만들 수 있다.
4. Cameras & Lenses
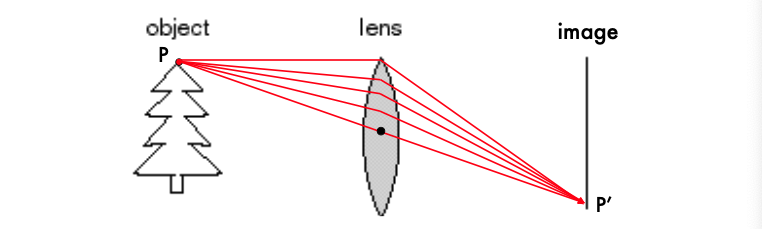 렌즈의 역할과 Focal Length(초점 거리): 렌즈의 기본 기능은 물체에서 나온 빛을 굴절시켜 필름이나 이미지 센서에 정확한 위치로 집중시키는 것이다. 이 과정을 통해 물체의 이미지가 필름에 형성된다.
렌즈의 역할과 Focal Length(초점 거리): 렌즈의 기본 기능은 물체에서 나온 빛을 굴절시켜 필름이나 이미지 센서에 정확한 위치로 집중시키는 것이다. 이 과정을 통해 물체의 이미지가 필름에 형성된다.
- 모든 광선은 렌즈의 중심축(광축 또는 주축)에 평행하게 수렴한다.
- 광축(렌즈의 중심축)에 평행하게 들어오는 모든 빛은 렌즈를 통과한 후, 렌즈의 중심에서 초점 거리 f만큼 떨어진 평면에 있는 한 점(초점)에 모인다.
- 이 초점에서 빛이 모이기 때문에 이미지는 선명하게 보인다.
- 렌즈의 중심을 통과하는 광선은 굴절되지 않는다.
- 렌즈의 중심을 통과하는 광선은 굴절되지 않고 그대로 직진한다. 렌즈가 왜곡 없이 이미지를 정확히 형성하도록 도와준다.
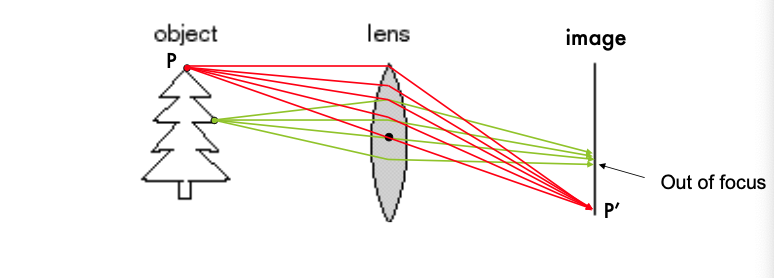
- “초점이 맞은 상태”
- 렌즈는 물체에서 반사된 빛을 굴절시켜 필름이나 이미지 센서에 초점을 맞춘다. 이 과정에서 특정 거리(초점 거리)에 있는 물체는 선명하게 “in focus”로 나타난다.
- “초점이 맞는” 특정 거리가 있다.
- 각 물체에는 렌즈의 초점 거리와 일치하는 특정 거리가 존재한다. 이 거리에 있는 물체만 선명하게 보이며, 이 거리보다 멀거나 가까운 물체는 흐릿하게 보일 수 있다.
- 심도(depth of field)와 관련이 있다.
- 심도: 렌즈가 특정 초점 거리를 기준으로 물체를 선명하게 잡을 수 있는 범위
- 심도가 깊을수록 더 넓은 범위의 물체가 선명하게 보이고, 심도가 얕을수록 특정 거리의 물체만 선명하게 보이며 나머지는 흐릿하게 보인다.
5. Lens Distortion
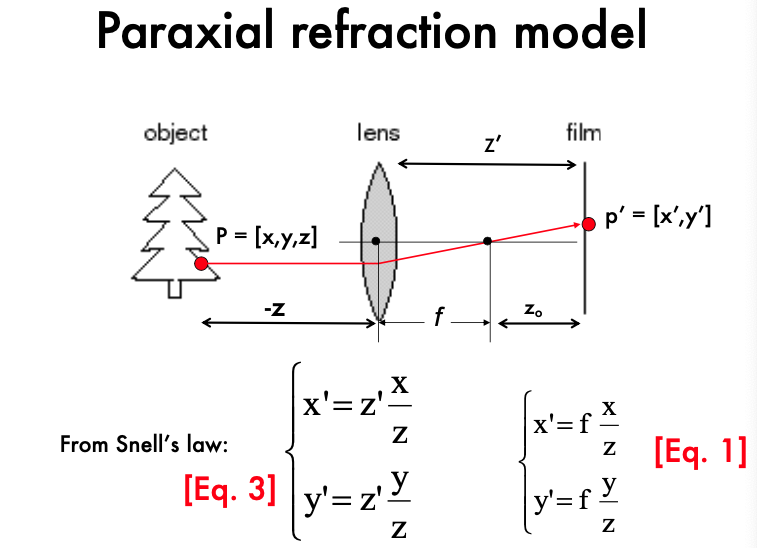
5.1 Paraxial Refraction Model (축소 굴절 모델)
- 이미지 형성 원리:
- 물체의 점 P(x, y, z)에서 나오는 빛은 렌즈를 통과하며 굴절되어 필름에 도달합니다.
- 이 과정에서 빛은 렌즈를 지나면서 축소되어 초점 거리에 따라 특정 위치(P’)에 이미지를 형성합니다.
- 기하학적 관계식:
- Snell의 법칙에 따라 물체의 좌표와 이미지 평면에 투영된 좌표 사이의 관계는 다음과 같은 수식으로 나타낼 수 있습니다:
- $ x’ = z’ \frac{x}{z} $
- $ y’ = z’ \frac{y}{z} $
- 여기서, z’는 물체의 이미지가 형성되는 위치로, 물체의 실제 위치 z와 렌즈의 초점 거리 f에 의해 결정됩니다.
- Snell의 법칙에 따라 물체의 좌표와 이미지 평면에 투영된 좌표 사이의 관계는 다음과 같은 수식으로 나타낼 수 있습니다:
- 초점 거리의 역할:
- 초점 거리 f는 렌즈의 중심에서 필름까지의 거리로, 이 거리에 따라 빛이 모이는 위치가 결정됩니다.
- 초점 거리가 짧을수록 빛이 더 빨리 모이고, 초점 거리가 길수록 빛이 멀리서 모입니다.
5.2 Radial Distortion (방사 왜곡)
- 왜곡의 발생:
- 렌즈를 통과하는 빛이 렌즈의 중심이 아닌 가장자리를 지나갈 때, 빛이 굴절되면서 이미지가 왜곡됩니다.
- 이러한 왜곡은 물체의 실제 형태와 다른 형태로 이미지가 형성되는 결과를 초래할 수 있습니다.
- 왜곡의 종류:
- Pin Cushion 왜곡: 이미지가 내부로 오목하게 왜곡되는 현상으로, 중심부가 확대되고 가장자리가 축소됩니다.
- Barrel 왜곡: 이미지가 외부로 볼록하게 왜곡되는 현상으로, 중심부가 축소되고 가장자리가 확대됩니다.
- 방사 왜곡의 영향:
- 렌즈의 왜곡은 이미지의 가장자리에서 가장 두드러지게 나타납니다.
- 이러한 왜곡은 이미지의 품질에 영향을 미치며, 특히 건축 사진이나 정밀한 측정이 필요한 경우 문제가 될 수 있습니다.
6. Intrinsic and Extrinsic Parameters:
- Intrinsic Parameters(내부 파라미터)와 Extrinsic Parameters(외부 파라미터)의 개념을 소개하고, 카메라 모델에서 이들이 어떻게 사용되는지 설명
- Camera Matrix(카메라 매트릭스)의 구성과 역할
7. 3D Transformations:
- 3D 공간에서의 Translation(이동), Scaling(스케일링), Rotation(회전) 변환을 다루며, 이들이 카메라 모델에서 어떻게 사용되는지 설명
- Homogeneous Coordinates(동차 좌표)를 사용하여 이러한 변환을 표현하는 방법
- Projective Transformations:
- Projective Transformation(사영 변환)의 개념을 소개하고, 이 변환이 이미지에서 어떻게 적용되는지
- 평행선이 이미지에서 Vanishing Point(소실점)에서 어떻게 만나게 되는지

1.triangulation(삼각측량)
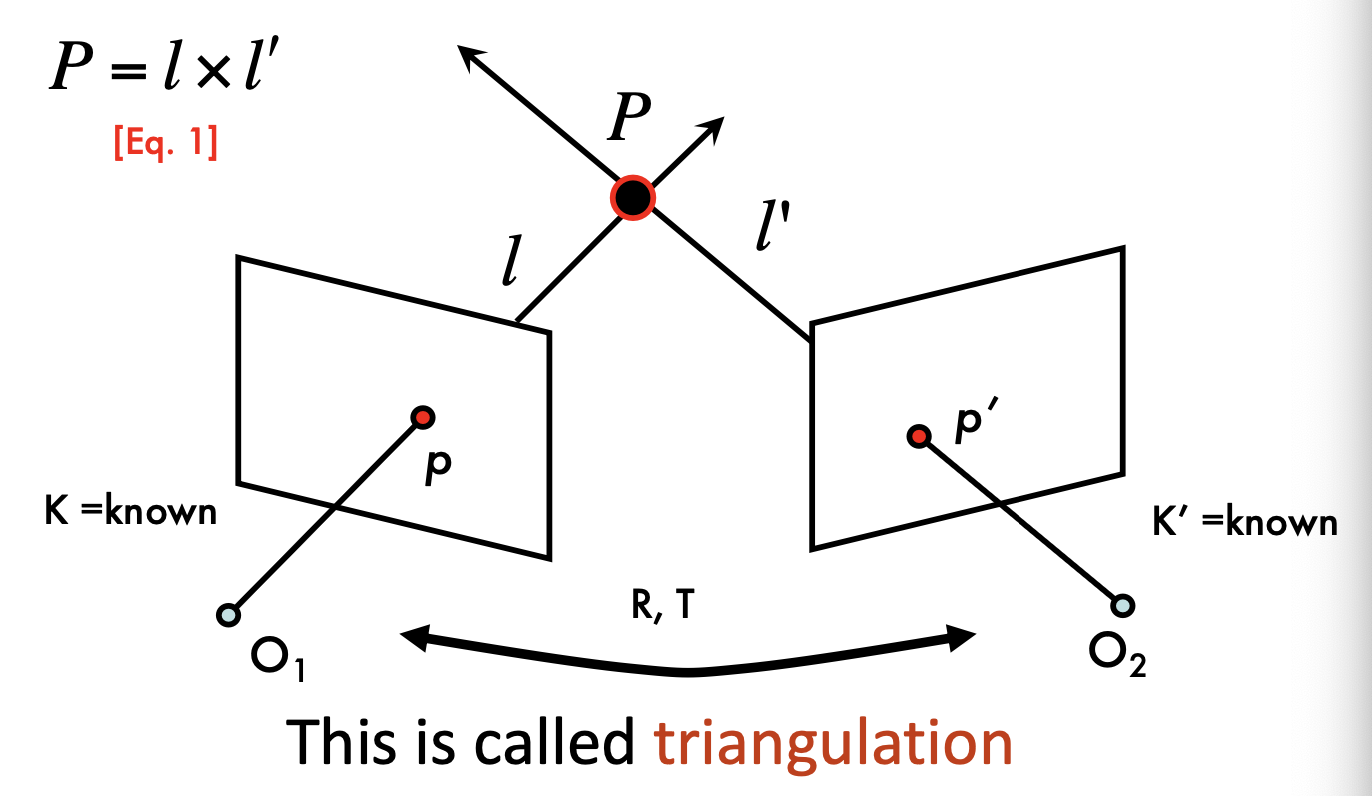 삼각측량은 두 개의 다른 관점(카메라 혹은 관찰점)에서 동일한 점을 관찰하여 그 점의 3차원 위치를 계산하는 기법이다.
두 개의 카메라 \(O_1\)과 \(O_2\)는 각각 평면 상의 점 \(p\)와 \(p'\)를 관찰하고, 이 두 점으로부터 3차원 공간의 점 \(P\)를 계산한다.
삼각측량은 두 개의 다른 관점(카메라 혹은 관찰점)에서 동일한 점을 관찰하여 그 점의 3차원 위치를 계산하는 기법이다.
두 개의 카메라 \(O_1\)과 \(O_2\)는 각각 평면 상의 점 \(p\)와 \(p'\)를 관찰하고, 이 두 점으로부터 3차원 공간의 점 \(P\)를 계산한다.
- \(P = l \times l'\) 두 직선 \(l\)과 \(l'\)의 교차점으로 3차원 점 \(P\)를 찾는 방법을 나타낸다. 이 교차점\(P\)가 삼각측량을 통해 구하고자 하는 3차원 위치이다.
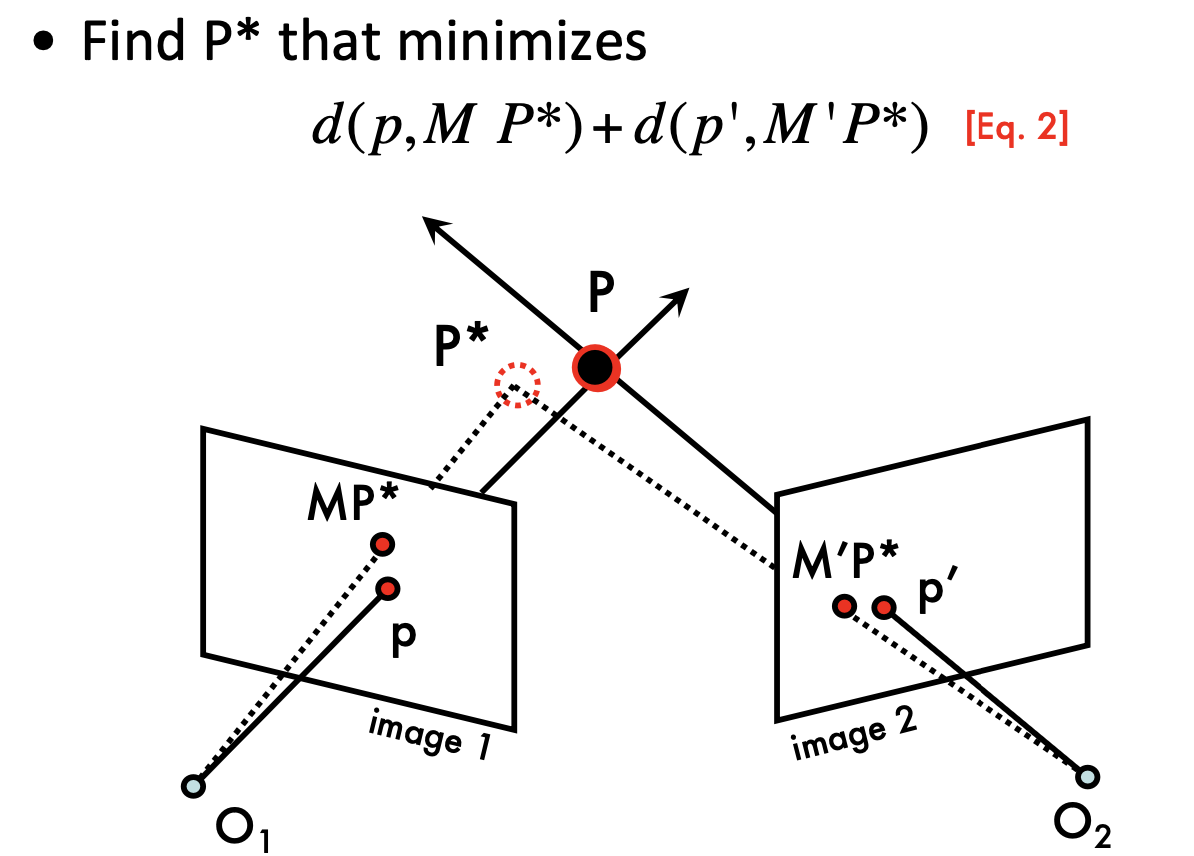
점 \(P\)의 추정된 위치를 \(P^*\)라고 하고, 이 \(P^*\)의 위치를 최적화하여 실질적인 점 \(P\)에 가장 가까운 위치를 찾는다. 최적화 문제의 목표는 두 이미지 평면에서의 예측된 점 \(MP^*\)와 \(M'P^*\)가 실제 관찰된 점 \(p\)와 \(p'\)에 최대한 가까워지도록 만드는 것이다.
방정식 \(d(p, MP^*) + d(p', M'P^*)\)는 이 과정에서 최소화해야 할 거리의 합이다. 두 이미지에서 예측된 점과 실제 점 사이의 유클리드 거리를 최소화하는 것을 목표로 한다. 이 과정을 통해 최적의 삼각측량 위치 \(P^*\)를 찾을 수 있다.
2.Multi (stereo)-view geometry
-
Camera geometry: 두 이미지에서 대응되는 점들이 주어졌을 때, 카메라 행렬, 위치, 자세를 찾는다. 카메라가 3차원 공간에서 어떻게 배치되고 방향이 정해졌는지를 결정하는 과정이다.
-
Scene geometry: 두 개 또는 그 이상의 이미지에서의 projection(투영)을 이용해 3D 공간에서 점의 좌표를 찾는 과정이다. 이는 삼각측량 방법 등을 사용해 해당 3차원 점의 정확한 위치를 계산한다.
-
Correspondence: 하나의 이미지에서 주어진 점 \(p\)에 대해, 다른 이미지에서 그에 대응하는 점 \(p'\)를 찾는다. 스테레오 비전에서 대응점을 정확하게 찾는 것이 이후의 3D 재구성이나 물체 추적 등에 매우 중요한 역할을 한다.
3.Epipolar geometry
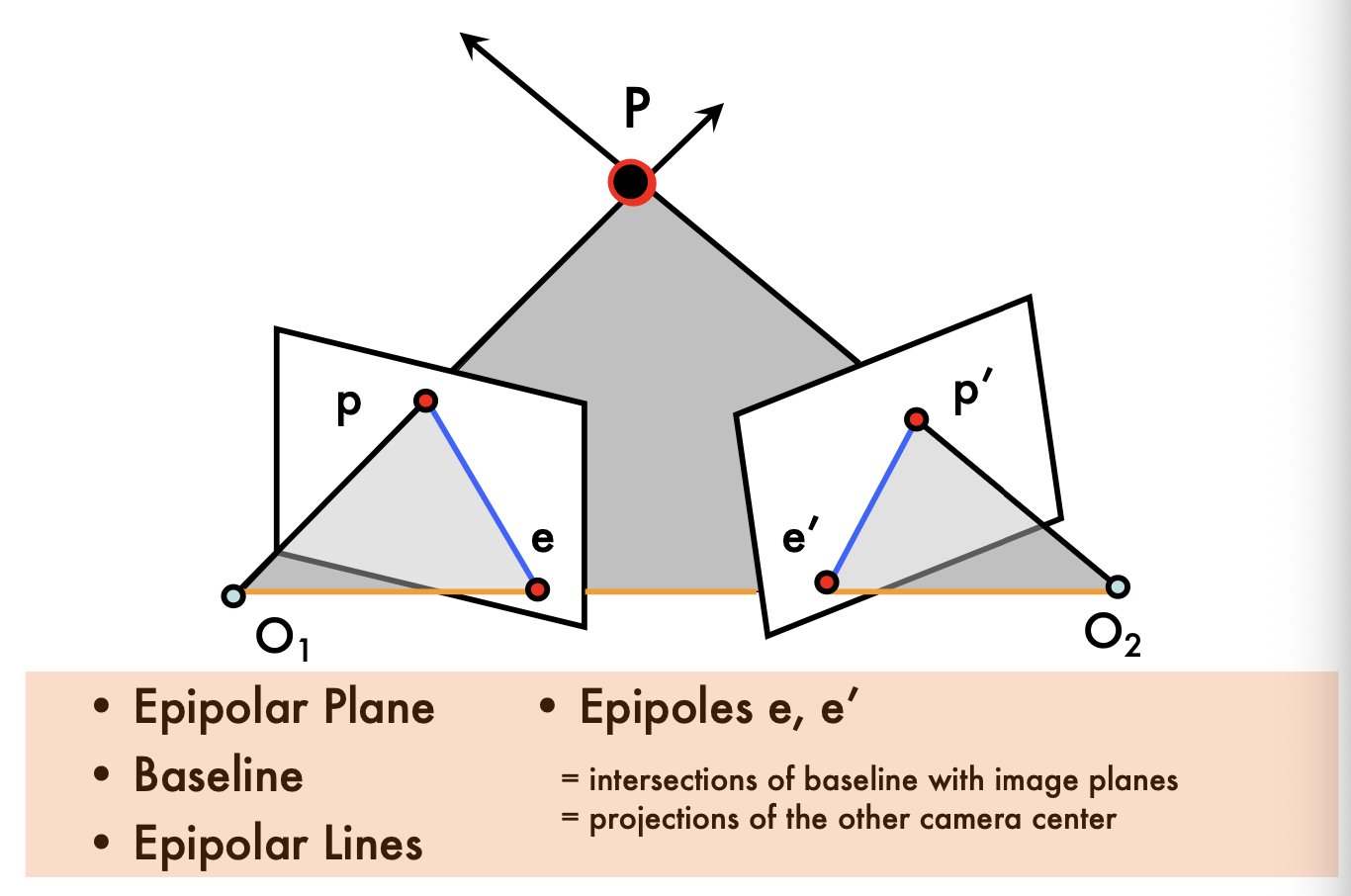 에피폴라 기하학은 두 개의 서로 다른 관점에서 동일한 3D 점을 관찰할 때 이미지 평면에서 발생하는 기하학적 관계를 다룬다.
에피폴라 기하학은 두 개의 서로 다른 관점에서 동일한 3D 점을 관찰할 때 이미지 평면에서 발생하는 기하학적 관계를 다룬다.
-
Epipolar Plane (에피폴라 평면): 두 카메라의 중심점 \(O_1\)과 \(O_2\) 그리고 3D 점 \(P\)를 포함하는 평면이다. 이 평면은 각 이미지 평면에서 에피폴라 선을 정의한다.
-
**Baseline **: 두 카메라 중심 \(O_1\)과 \(O_2\)를 연결하는 선이다.
-
Epipolar Lines (에피폴라 선): 에피폴라 평면이 이미지 평면과 만나는 선이다. 각각의 이미지에서 점 \(P\)가 에피폴라 선 위에 투영된다. 한 이미지에서 점을 선택하면 다른 이미지에서 그에 대응하는 점은 반드시 에피폴라 선 위에 존재해야 한다. 이 특성은 스테레오 매칭 알고리즘에서 계산량을 줄이는 데 매우 유용하다.
-
Epipoles (에피폴 \(e, e'\)): 에피폴은 base line이 이미지 평면과 교차하는 점이다. 또한, 하나의 카메라의 중심점이 다른 카메라의 이미지 평면에 투영된 지점이다. 이 점들은 에피폴라 선들의 교차점이며, 모든 에피폴라 선들이 이 점을 지나간다.
3.1 Parallel Image Planes
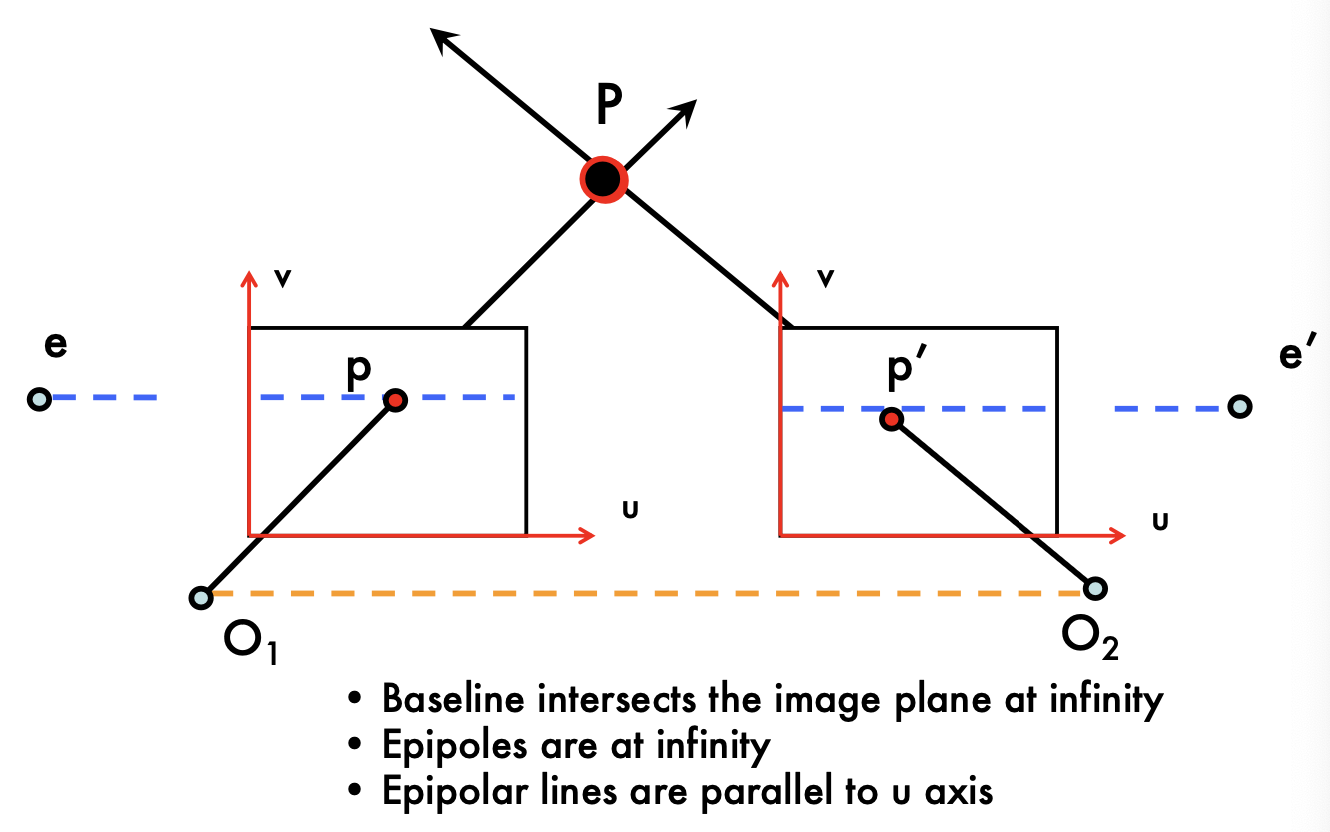
- 두 이미지 평면이 서로 평행한 경우다.
에피폴들은 무한대에 위치하며, 에피폴라 선은 u축에 평행하게 나타난다.

- 예시는 실제 건물 이미지를 통해, 두 이미지 간의 대응점들이 수평선(에피폴라 선)을 따라 어떻게 일치하는지 보여준다.
3.2 Forward Translation:
- 설명: 카메라가 전방으로 이동하는 경우를 설명합니다. 이 경우, 두 이미지에서 에피폴들은 동일한 위치에 있으며, 이는 “확장점(Focus of Expansion, FOE)”이라고 불립니다.
- 예시: 복도 이미지를 사용하여, 전방 이동 시 발생하는 시각적 확장 효과를 나타냅니다.
3.3 Epipolar Constraint:
- 설명: 한 이미지에서 특정 점 ( p )이 주어졌을 때, 다른 이미지에서 대응하는 점 ( p’ )이 에피폴라 선을 따라 위치하게 된다는 제약 조건을 설명합니다.
- 예시: 조각상의 얼굴을 예로 들어, 첫 번째 이미지에서 선택한 점의 대응점을 두 번째 이미지에서 찾는 과정을 보여줍니다.
3.4 Epipolar Geometry:
- 설명: 에피폴라 기하학의 기본적인 설정을 시각적으로 나타낸 것입니다. 두 이미지 평면과 에피폴라 평면 간의 관계를 보여주며, 에피폴라 선들이 두 이미지 평면에서 어떻게 형성되는지를 설명합니다.
- 예시: 이전 이미지에서 사용된 조각상 예제를 통해, 에피폴라 선과 그에 따른 대응점을 시각화합니다.