Retrospectives Badge

epipolar geometry는 두 view 사이의 intrinsic projective geometry이다. epipolar geometry는 scene structure에 독립적인 반면 오직 cameras의 internal parameters와 relative pose에 의존한다.

fundamental matrix F 는 이intrinsic geometry를 반영한다. F는 두 이미지 사이의 고유한 기하학적 관계를 요약하는 3x3 행렬로, 랭크는 2다.

1 Stereo systems

1.1 Rectification(정렬)

두 이미지가 Affine 카메라로 잘 근사될 수 있을 때, 이미지를 Affine 변환만으로 보정할 수 있다. Affine Fundamental Matrix를 사용하여 두 이미지 간의 대응 관계를 설정하고, 이미지를 보정하는 방법(parallel image로 만드는 등) rectification을 알기 전, 먼저 morphing에 대해 알아보자!

1.1.1 View Morphing

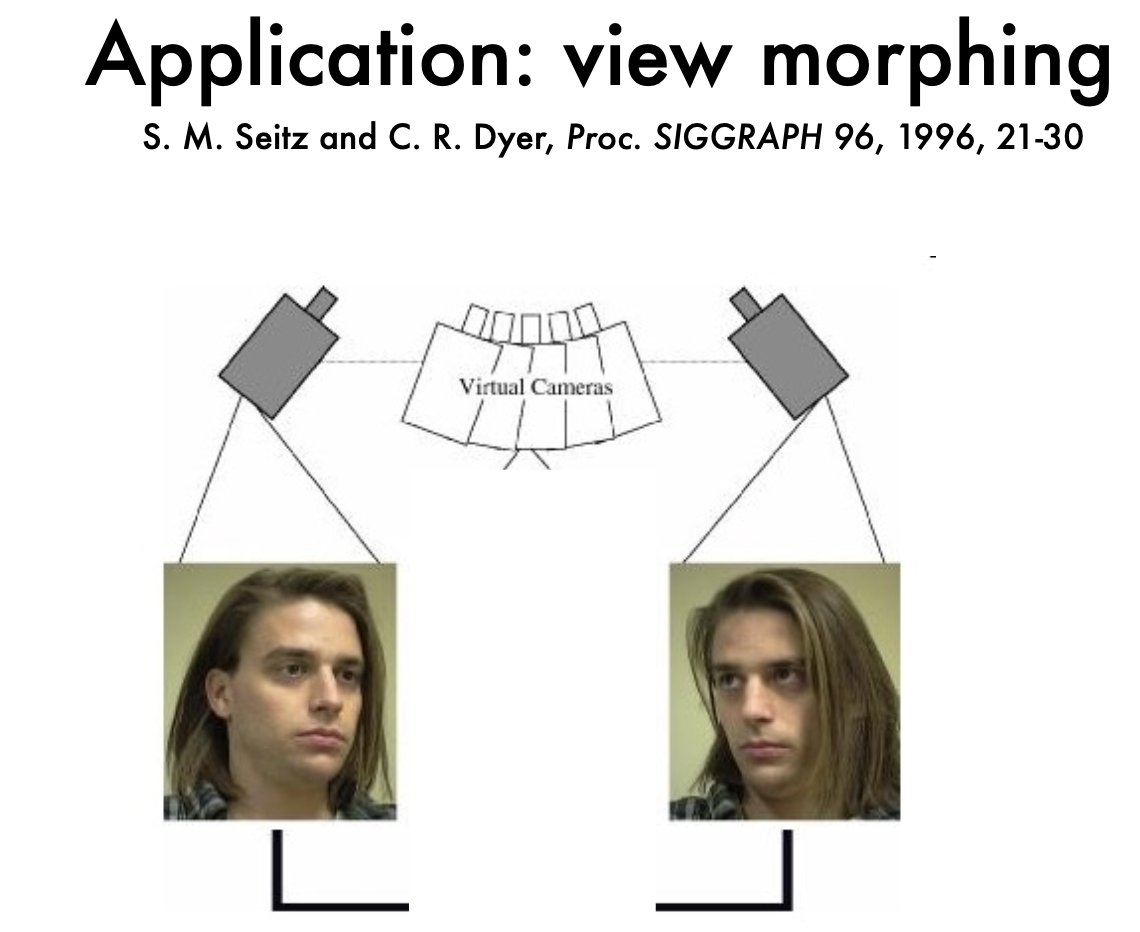두 개의 실제 카메라에서 촬영된 이미지 간에 새로운 뷰를 생성한다. 두 이미지 사이의 가상의 카메라 뷰를 생성함으로써 부드럽게 두 장면 간의 변형(morphing)을 구현한다.

1.1.2 Rectification

서로 다른 두 카메라에서 촬영된 이미지가 동일한 평면에 위치한 것처럼 변환하는 과정이다. 두 이미지 간의 대응점을 찾는 과정을 단순화시켜서 View Morphing에서 매우 중요한 역할을 한다. 정렬을 하는 이유는 이미지의 대응점을 직선 상에 맞춰서 대응점을 찾기 위함이다. View morphing에서 두 이미지를 자연스럽게 변환하기 위한 가장 첫걸음이라고 할 수 있다.

1.1.3 Deep View Morphing

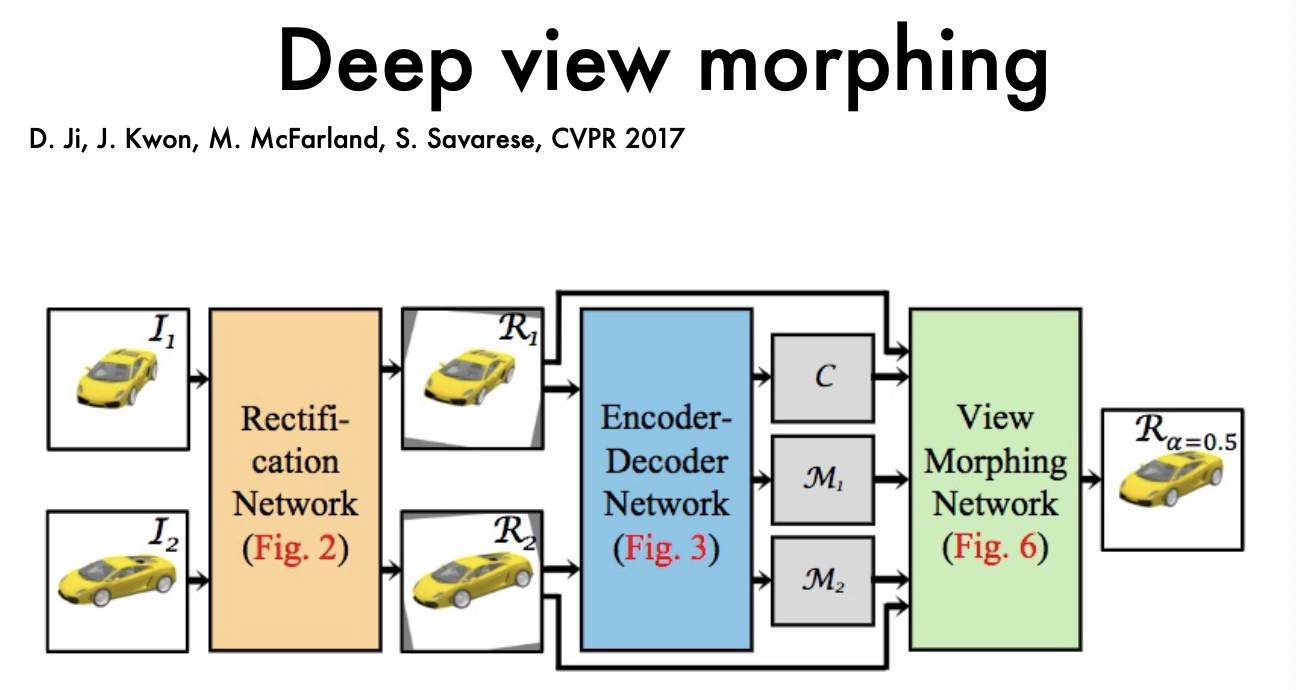인코더-디코더 구조로 이미지 간의 변환을 더 정교하게 구현한다. 네트워크 구조는

  • Rectification Network: 입력된 두 이미지를 정렬하는 네트워크. 두 이미지 간의 기하학적 불일치를 제거
  • Encoder-Decoder Network: 입력된 정렬된 이미지를 기반으로 중간 뷰를 생성
  • View Morphing Network: 두 정렬된 이미지 간의 자연스러운 전환을 구현

    1.2 Correspondence problem

    Correspondence Problem(대응 문제)은 스테레오 비전(Stereo Vision)에서 매우 중요한 역할을 하며, 두 이미지 간의 대응점을 찾는 과정이다.

1.2.1 Correspondence Problem (대응 문제)

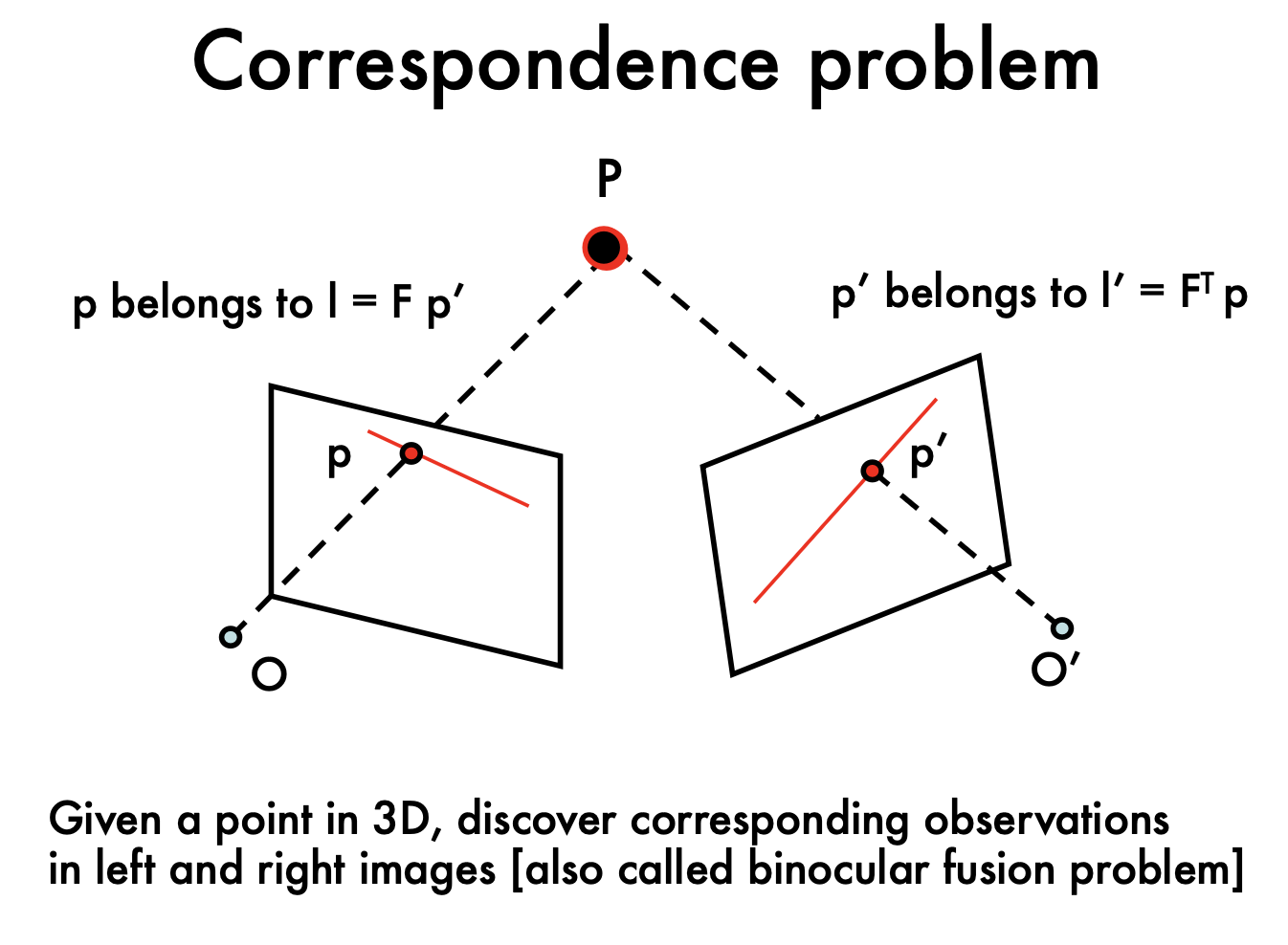3D 공간에 있는 점 \(P\)가 두 이미지에서 각각의 점 \(p\)와 \(p'\)로 투영 될 때 두 점 사이의 대응관계를 찾는 것이 correspondence problem이다. stereo vision에서 두 카메라가 동일한 3D 지점을 다른 위치에서 촬영했을 때, 두 이미지에서 같은 3D 지점을 찾는 문제와 같다.

  • 에피폴라 제약: 두 이미지에서 각각의 점 \(p\)와 \(p'\)는 특정한 기하학적 제약을 따른다. 점 \(p\)는 에피폴라인(epipolar line) 위에 존재해야 한다. (두 이미지 사이의 대응점을 찾기 위해) \(p\)는 \(F \cdot p'\)에 의해 정의된 에피폴라인 \(l\) 위에 속해야 하며, \(p'\)도 마찬가지로 \(F^T \cdot p\)에 의해 정의된 라인 위에 있어야 한다. 여기서 \(F\)는 기본 행렬(Fundamental Matrix)로, 두 이미지 간의 기하학적 관계를 나타낸다.

2. Rectified

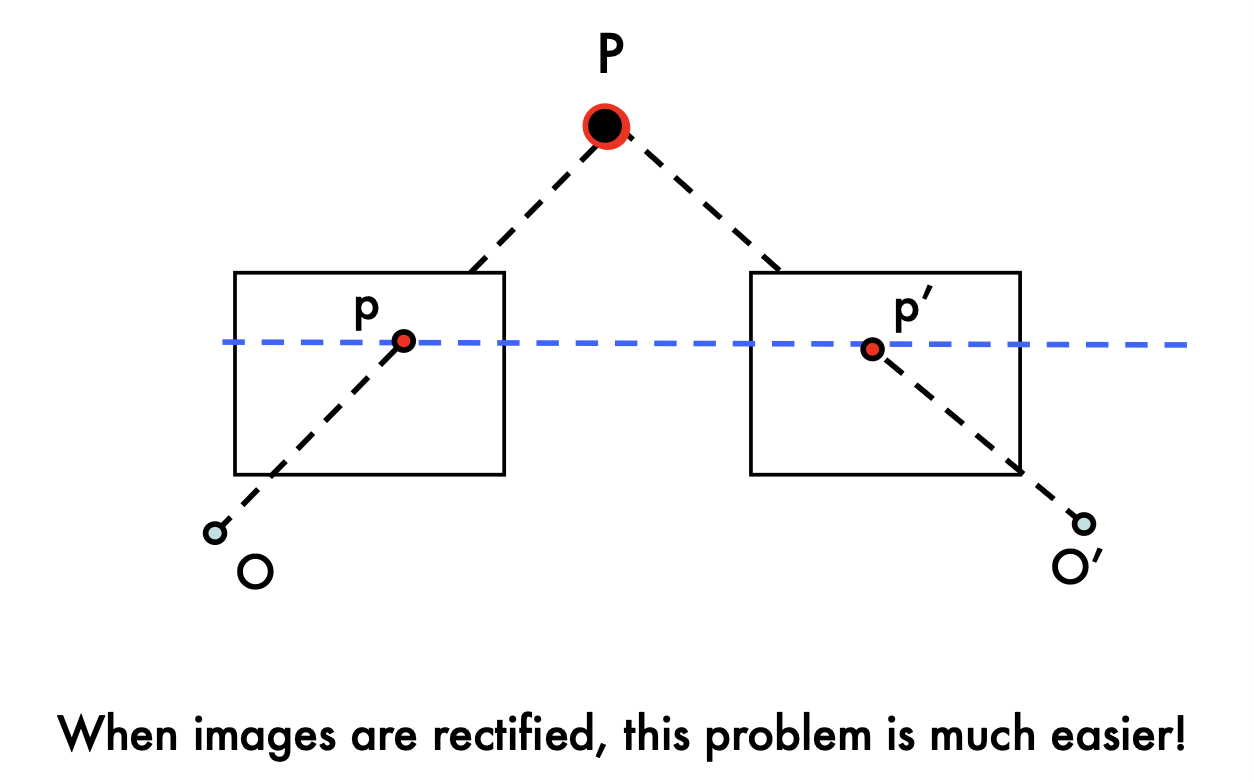이미지가 rectified되었을 때, 대응 문제를 훨씬 더 쉽게 해결할 수 있다. 두 이미지가 동일한 평면에서 촬영된 것처럼 기하학적으로 변환해서 각 이미지에서 대응점들이 동일한 행(수평선) 상에 놓이게 된다. 이로 인해 복잡한 2D 계산 없이 대응점을 찾을 수 있다.

  • 대응점: 정렬된 상태에서는 대응 문제의 난이도가 크게 줄어들며, 이를 통해 스테레오 비전에서 대응점을 빠르고 효율적으로 찾을 수 있다.

    2 Multi-view geometry

    2.1 The SfM problem

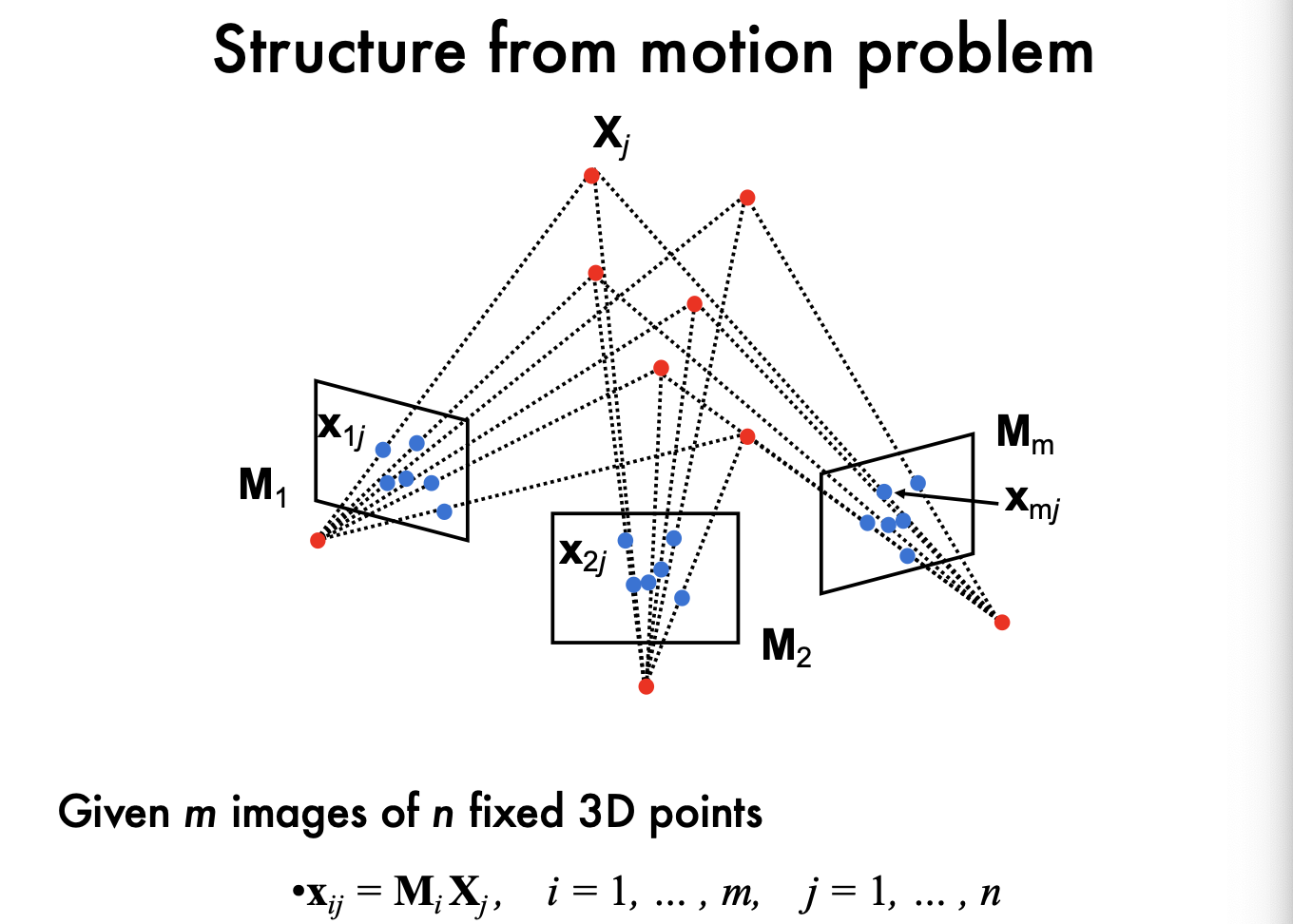    Structure from Motion, SfM

    2.1.1 Structure from motion problem

    SfM problem

  • 주어진 \(m\)개의 이미지에서 \(n\)개의 고정된 3D 점들의 관측치를 바탕으로, 각 이미지의 투영 행렬 \(M_i\)와 3D 점 \(X_j\)를 추정하는 문제다. \(x_{ij} = M_i X_j\)로 주어진 수식은 각 이미지 \(i\)에서 점 \(j\)가 어떻게 보이는지를 나타낸다. 관측치를 통해 카메라의 투영 행렬과 3D 점들의 위치를 추정한다.

    2.1.2 Affine Structure from Motion

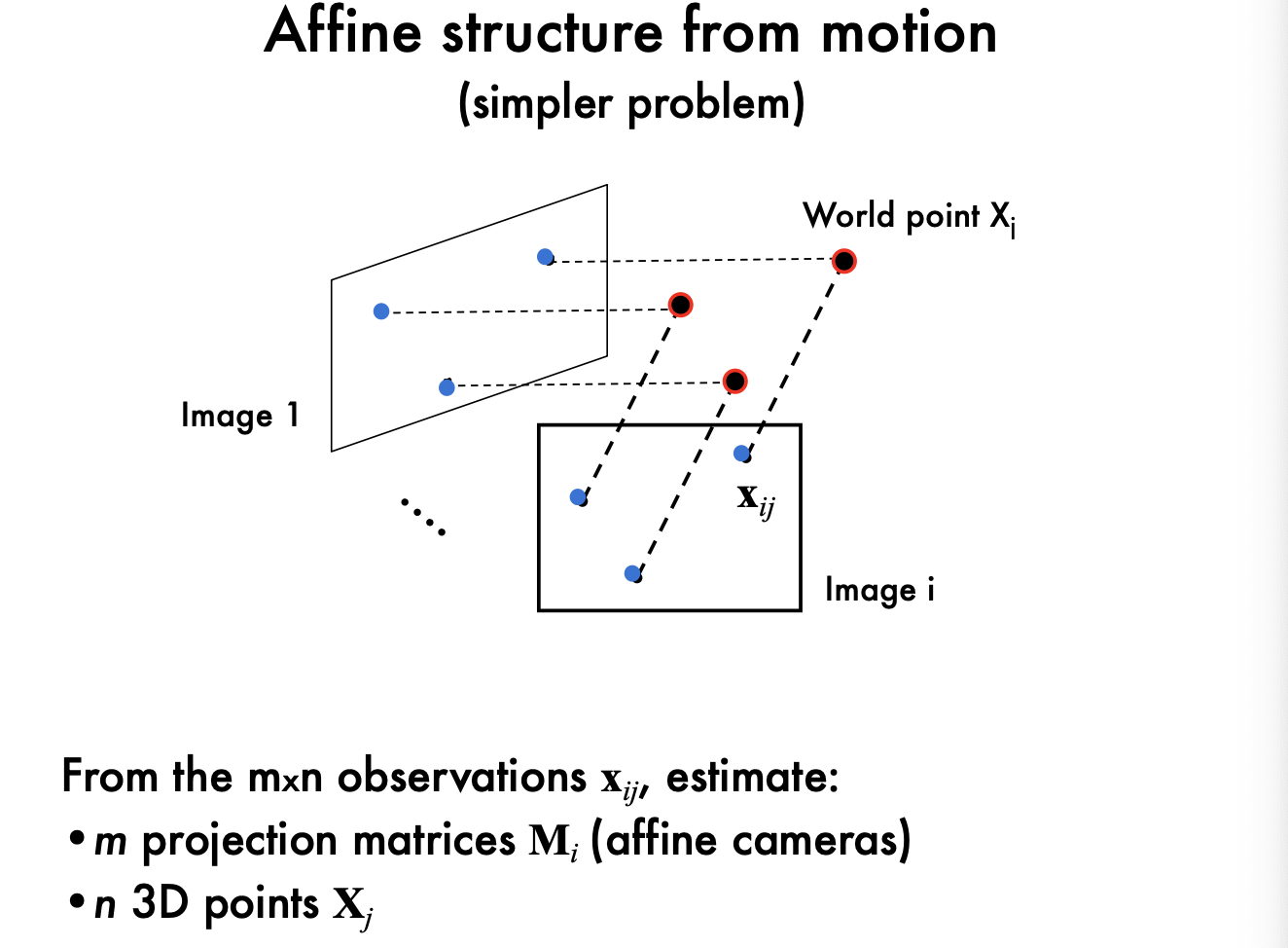    원래의 SfM 문제에서 조금 더 간단한 경우다. Affine camera를 가정하여 문제를 해결하는 방식이다.

  • Affine model: Affine 카메라 모델은 원근 투영을 고려하지 않는 간단한 모델이다. 각 카메라에서 점이 어떻게 보이는지를 직선 관계로 나타낸다. 투영 행렬과 3D 점의 위치를 추정하는 문제를 해결한다. \(x_{ij} = A_i X_j + b_i\)에서 \(A_i\)는 Affine 투영 행렬이고, \(b_i\)는 변환 벡터다.

2.1.3 Perspective vs Affine 모델

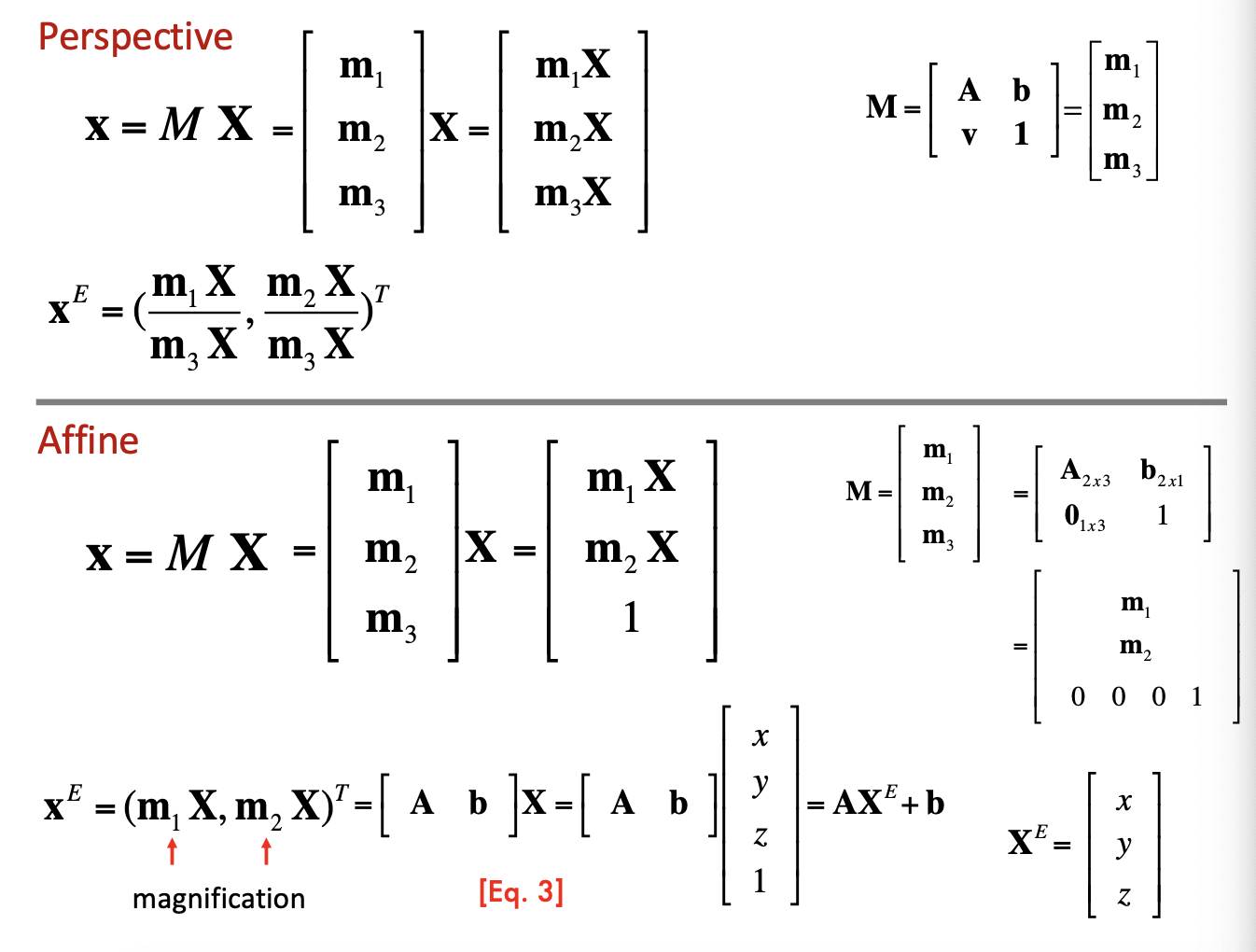원근 투영(Perspective)과 Affine 카메라 모델의 차이 Perspective 모델: 투영된 이미지 좌표가 3D 좌표의 비율로 결정된다. Affine 모델: 원근 왜곡을 무시한다. 선형적인 관계를 가정한다.

  • Perspective 모델은 좀 더 복잡한 계산을 필요로 하지만 현실적인 카메라의 동작을 더 잘 설명한다. Affine 모델은 좀 더 간단하지만, 실제 상황에서의 정확성은 떨어질 수 있다.

2.1.4 Affine 카메라의 특성

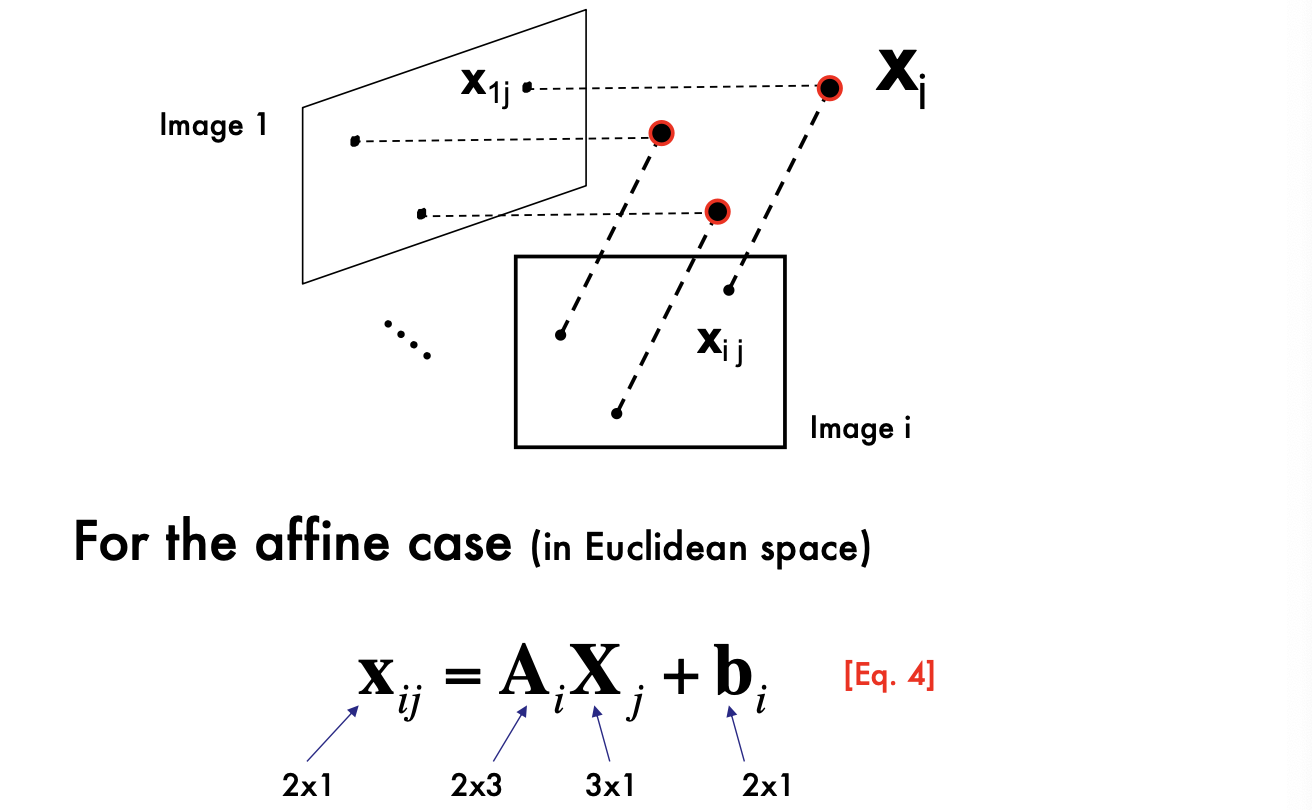Affine 카메라에서는 카메라 행렬 \(A_i\)와 변환 벡터 \(b_i\)를 통해 이미지에서의 점들을 설명할 수 있다. 관측값 \(x_{ij}\)으로부터 Affine 투영 행렬 \(A_i\), 변환 벡터 \(b_i\), 그리고 3D 좌표 \(X_j\)를 추정한다.

2.1.5 Affine Rectification

두 이미지가 Affine 카메라로 잘 근사될 수 있을 때, 이미지를 Affine 변환만으로 보정할 수 있다. Affine Fundamental Matrix를 사용하여 두 이미지 간의 대응 관계를 설정하고, 이미지를 보정한다.!

2.2 Affine SfM

\(m\)개의 이미지에서 \(n\)개의 고정된 3D 점 \(X_j\)에 대한 관측값 \(x_{ij}\)가 주어졌을 때. \(x_{ij} = A_i X_j + b_i\) \(i = 1, ..., m\)(카메라의 개수), \(j = 1, ..., n\) (3D 점의 개수).

  • \(A_i\)는 Affine 카메라의 투영 행렬, \(b_i\)는 변환 벡터.

\(m\)개의 투영 행렬\(A_i\), 변환 벡터 \(b_i\), 그리고 3D 점들의 위치 \(X_j\)를 추정한다.

  • \(x_{ij}\)는 \(m \times n\)개의 관측값으로 구성되어 있다.

각 카메라에서의 3D 점의 투영을 모델링한다. 그래서 역으로 카메라의 위치와 3D 구조를 추정한다. Affine SfM은 실제 카메라의 원근 효과를 무시하는 대신 간단한 선형 모델을 사용하여 문제를 해결하는 방법이다.