1. 마스터클래스(오태현교수님)

1. 기술의 발전

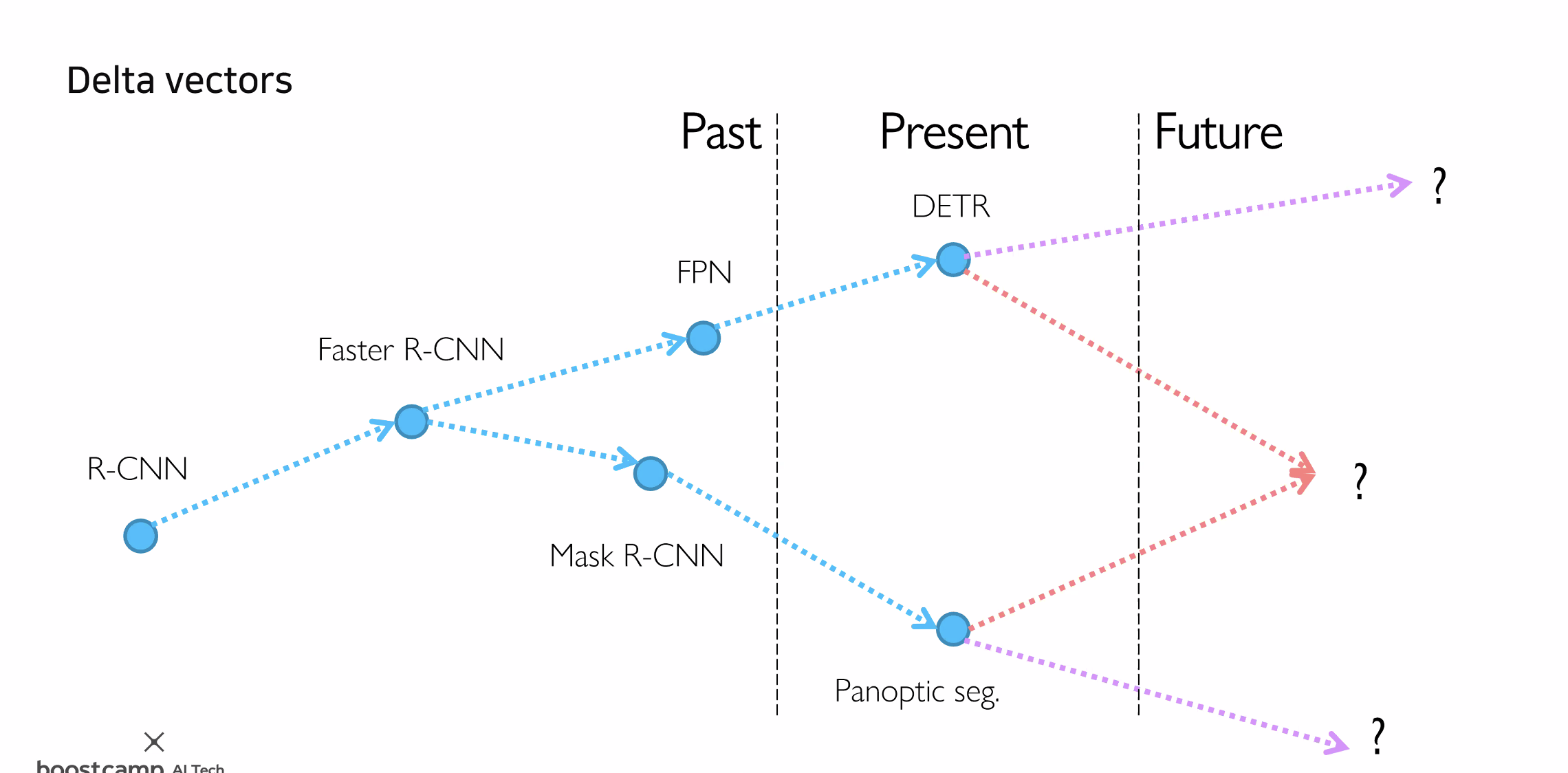AI 기술의 발전은 단계적으로 이루어져 왔습니다. 다양한 개념들이 각각의 기술로 발전하고, 서로 다른 AI 개념들이 통합되면서 더욱 정교한 시스템으로 진화하고 있습니다. 예를 들어, 이미지에서 객체를 탐지하는 기술과 텍스트에서 의미를 분석하는 기술이 결합되면, 이미지를 설명하는 자연어 생성 시스템으로 확장될 수 있습니다. 이러한 탐지 기술은 특히 의료, 보안, 자율주행 등에서 활용되고 있습니다.

2. 논문 선정 및 분석 방법

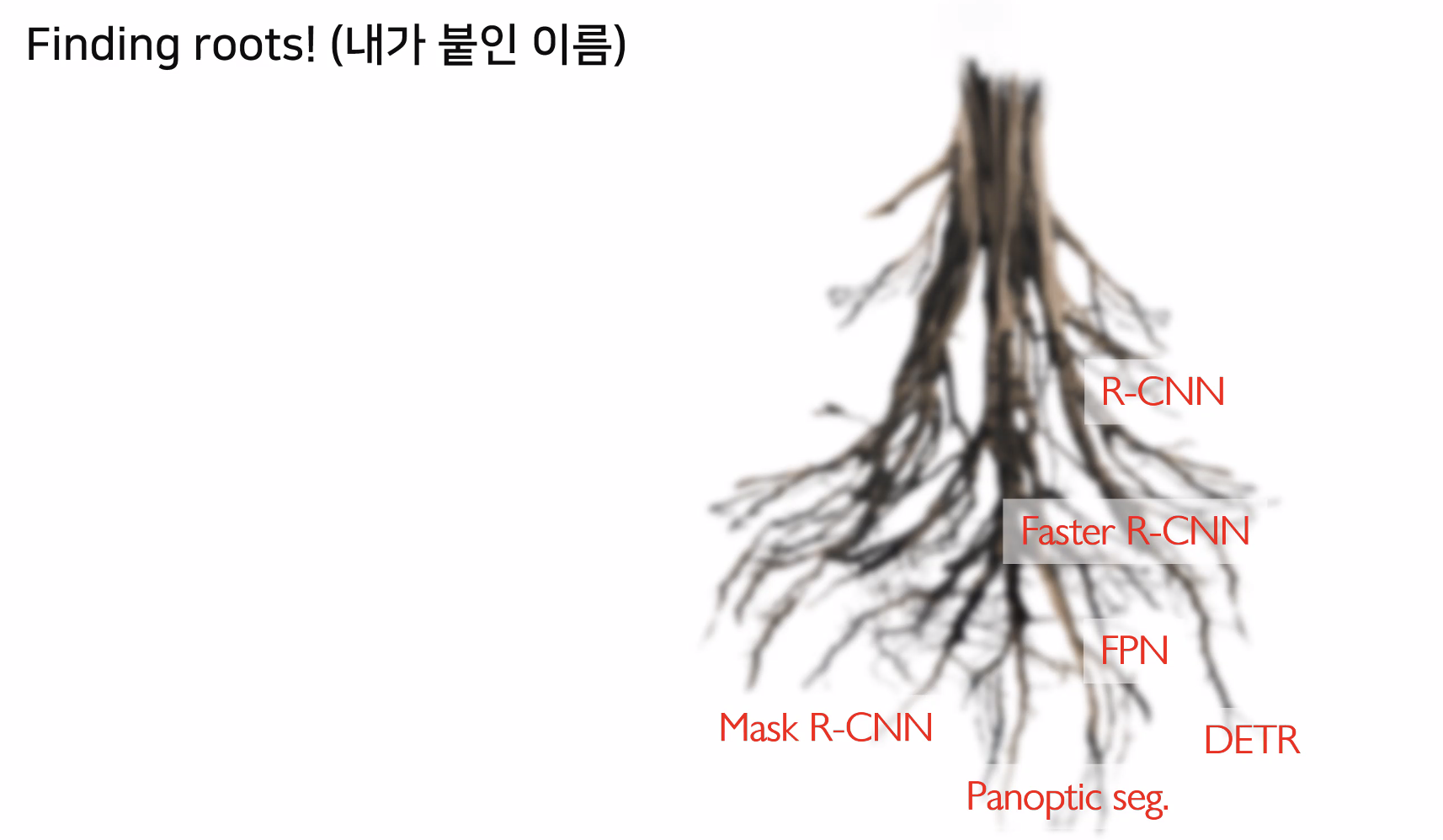AI 분야는 매일 새로운 논문이 쏟아지는 만큼, 모든 논문을 읽기 어렵습니다. 효율적인 논문 선정법으로는 최신 연구에서 자주 인용되는 핵심 논문들을 중심으로 관련 연구들을 추적하는 방법이 있습니다. 중요한 논문들은 서로 클러스터링되어 있으며, 이를 통해 현재의 State-of-the-Art(SOTA) 기술이 어떻게 발전했는지 이해할 수 있습니다. 관련된 연구 작업을 통해 과거와 현재의 중요한 논문들을 분석하고, 자신의 연구 주제에 맞는 최신 논문을 선택하여 집중적으로 읽는 것이 좋습니다.

3. Trend 1: Foundation Models

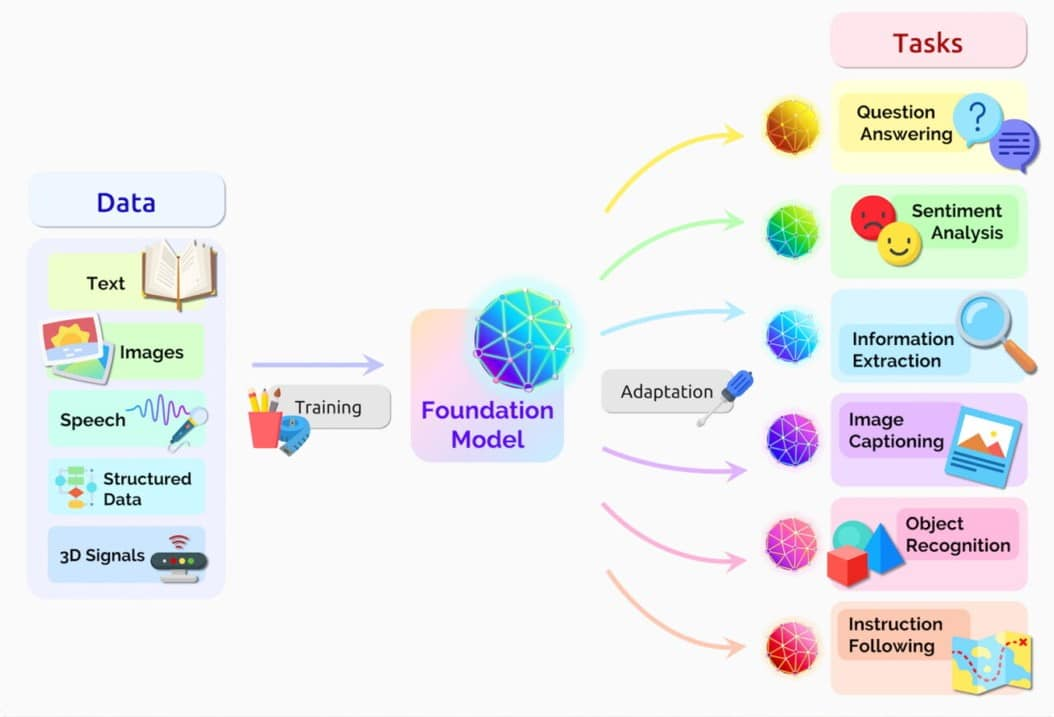“Foundation Models”는 대규모 데이터로 학습된 모델을 의미하며, 다양한 작업에 적용 가능한 범용 모델입니다. 대표적으로 GPT-4나 BERT 등이 이에 해당합니다. 이 모델들은 거대한 데이터 세트에서 훈련되어 다양한 분야에 걸쳐 높은 성능을 보여줍니다. 이러한 모델들은 특정 작업에 맞춘 미세 조정을 통해 다양한 응용 분야에서 사용됩니다.

4. Trend 2: Text-to-X

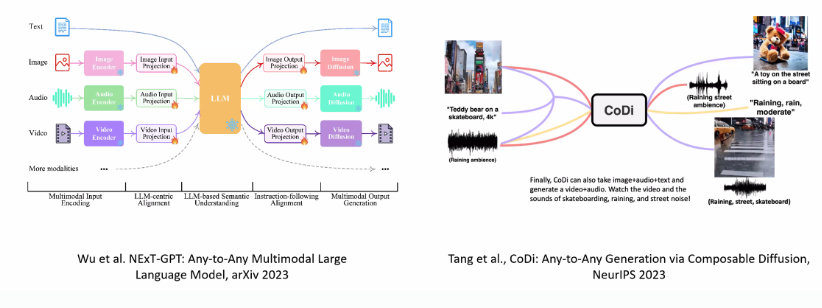Text-to-X는 텍스트 입력을 기반으로 다양한 결과물을 생성하는 기술을 의미합니다. Text-to-Image, Text-to-Speech, Text-to-Video 등이 이에 해당하며, 텍스트로부터 이미지나 음성, 영상 등의 결과물을 생성하는 기술입니다. 이러한 기술은 이미지 생성 AI인 DALL-E, 영상 생성 AI 등에서 볼 수 있듯이, 콘텐츠 생성과 창작 분야에서 혁신적인 변화를 가져오고 있습니다.

5. Trend 3: ChatGPT와 Multimodal AI

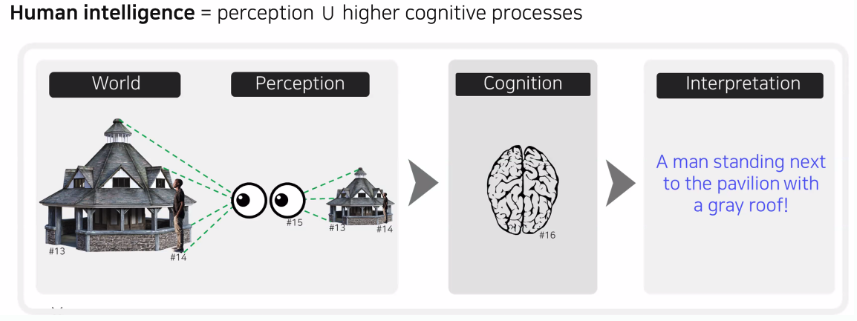ChatGPT와 같은 LLM(Large Language Models)은 언어 처리에 있어 상당한 발전을 이루었지만, 언어로 표현되지 않는 물체나 상황을 이해하기에는 한계가 있습니다. 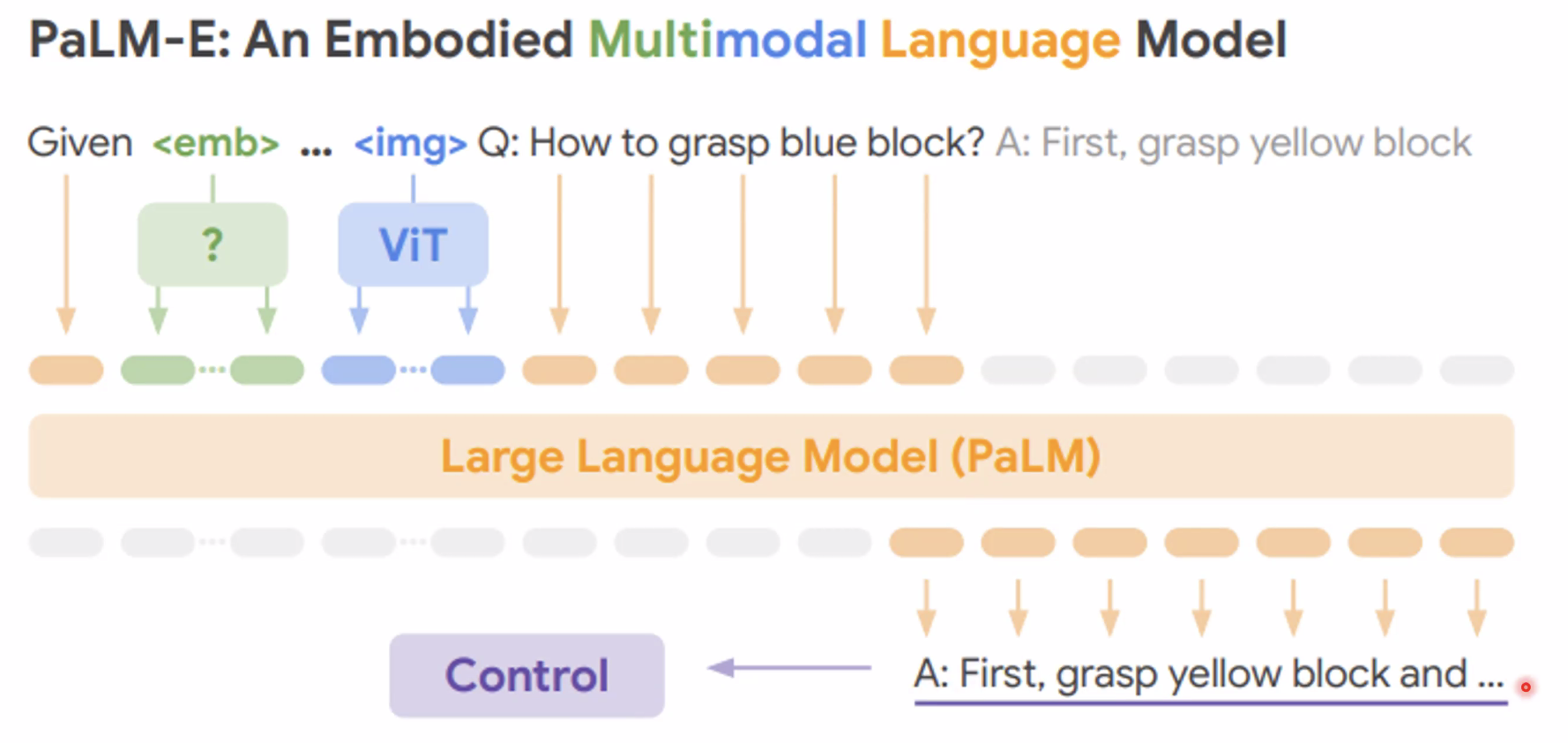이를 보완하기 위해 멀티모달 AI가 주목받고 있습니다. 멀티모달 AI는 텍스트, 이미지, 음성 등 여러 형식의 데이터를 동시에 처리하여 더 복잡하고 현실적인 문제를 해결할 수 있습니다. 예를 들어, 언어뿐만 아니라 이미지나 동작 신호까지 함께 이해하고 처리할 수 있는 AI가 개발되고 있습니다.

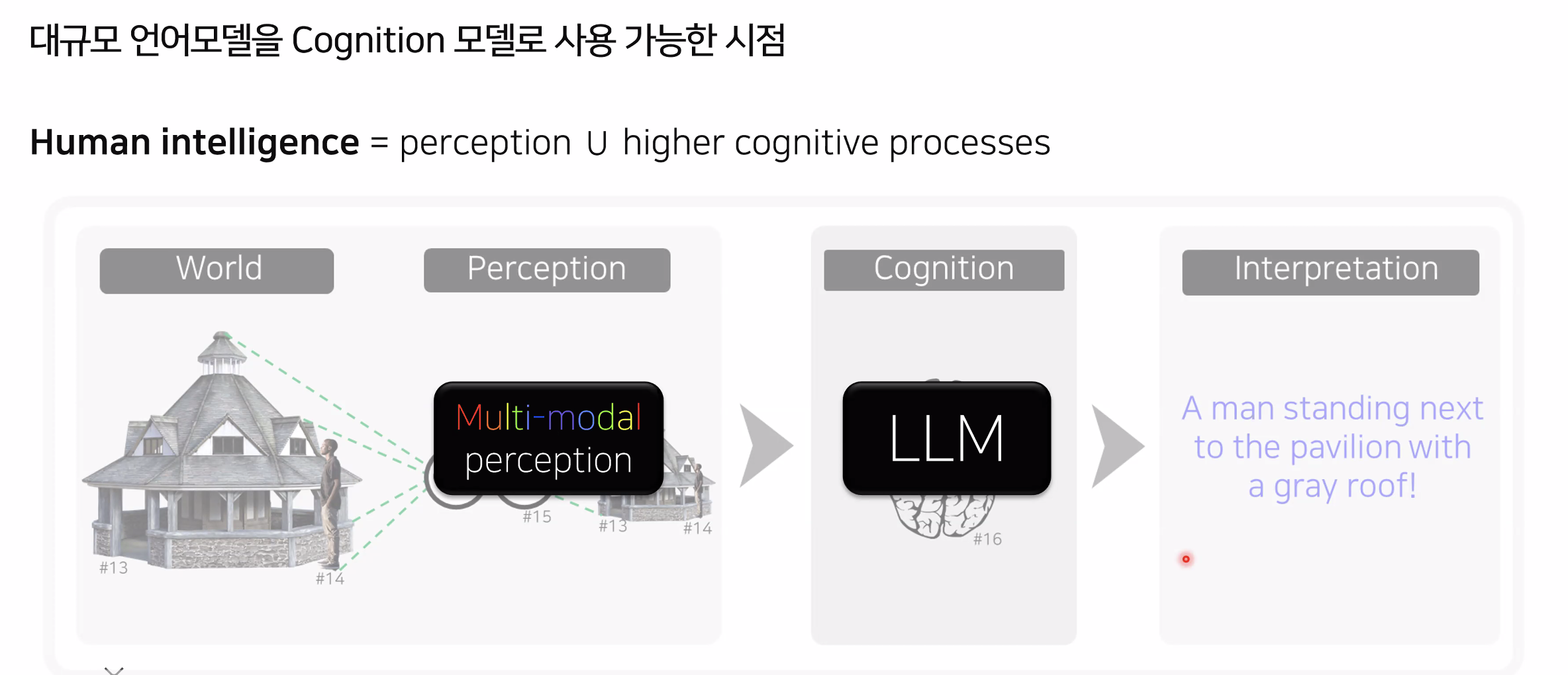
6. AGI (Artificial General Intelligence)

현재는 AGI(인공지능 일반, 즉 사람처럼 모든 지적 작업을 수행할 수 있는 AI)의 구현을 테스트하는 단계에 이르고 있습니다. AGI는 특정한 작업에 국한되지 않고 다양한 문제를 해결할 수 있는 범용 인공지능을 의미합니다. 이러한 기술은 아직 개발 중이지만, 대규모 언어 모델과 멀티모달 AI의 발전이 AGI로 향하는 중요한 단계가 되고 있습니다.

2. 피어세션 시간 DDPM

DDPM(Denoising Diffusion Probabilistic Models)은 생성 모델의 한 종류로, 노이즈를 점진적으로 추가한 데이터에서 원래 데이터를 복원하는 방식으로 학습 및 샘플링을 진행합니다. 이 과정은 두 단계로 나눌 수 있습니다: Forward Process와 Reverse Process. 아래에서는 수학적으로 각 과정을 설명하겠습니다.

1. Forward Process (노이즈 추가 단계)

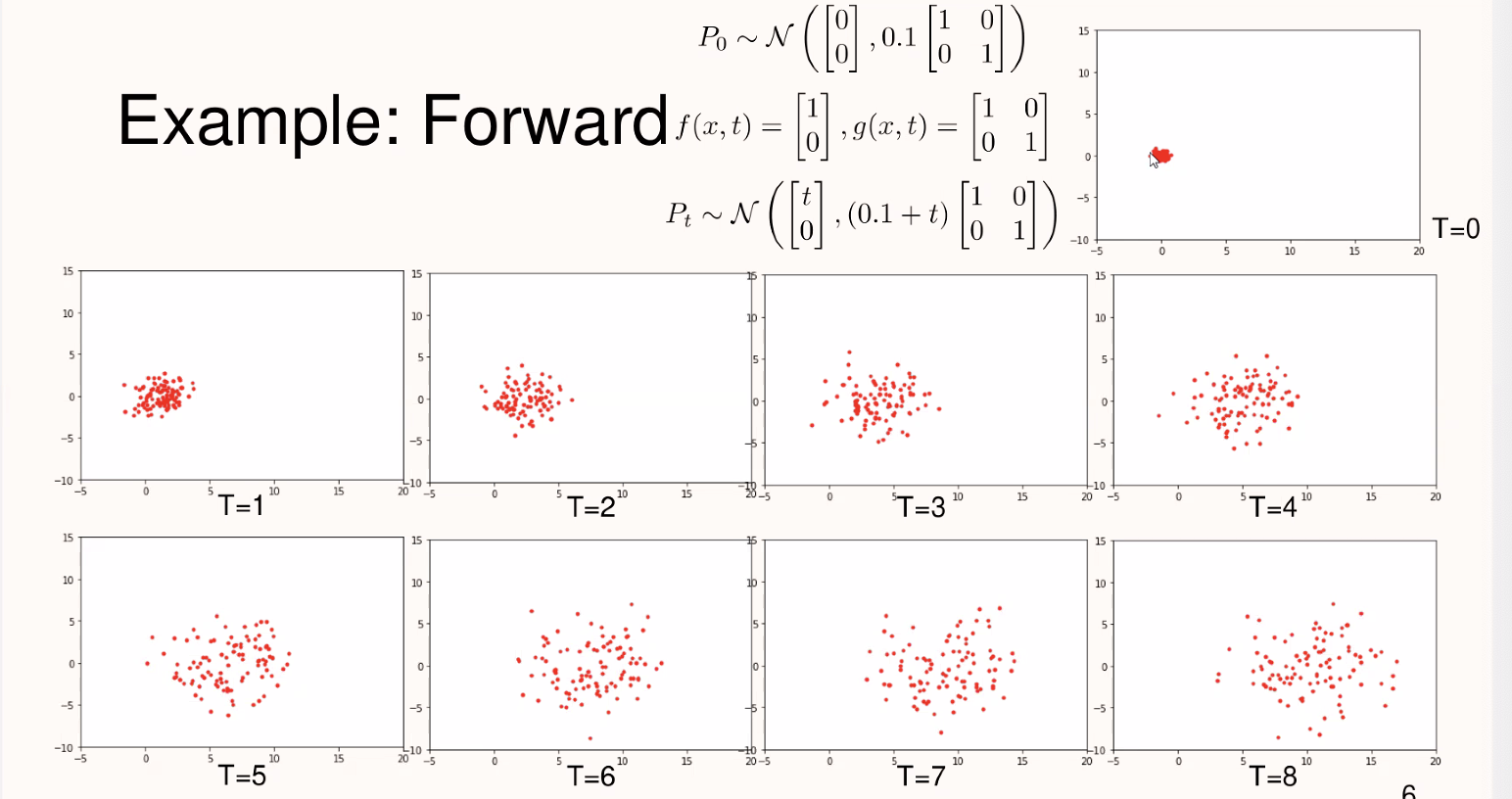
Forward Process에서는 원래 데이터에 점진적으로 가우시안 노이즈를 추가합니다. 그림에서는 각 타임스텝$T$에서 데이터에 노이즈가 더해지며 점점 퍼지는 분포를 볼 수 있습니다.

수식: 주어진 데이터$x_0$에 대해, Forward Process는 각 시간$t$에서 데이터$x_t$를 아래와 같이 정의된 노이즈 추가 과정에 따라 생성합니다:

\[q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I)\]

여기서$\beta_t$는 각 타임스텝에서의 노이즈의 크기를 나타냅니다. 이 노이즈는 가우시안 분포$\mathcal{N}$에 따라 추가되며,$x_{t-1}$에 점점 더 많은 노이즈가 추가됨에 따라$x_t$는 원래 데이터$x_0$와 멀어지게 됩니다.

Forward Process에서 중요한 수식

Forward Process는 일반적으로 데이터에 노이즈를 추가하는 과정입니다.$x_0$에 대해,$x_T$는 순수한 노이즈로 변하게 됩니다. 이를 요약하면:

[ q(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I) ]

여기서,$\alpha_t = 1 - \beta_t$,$\bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s$입니다. 이 수식은 데이터가 시간이 지남에 따라 점진적으로 노이즈로 변하는 과정을 설명합니다.

2. Reverse Process (노이즈 제거 단계)

Reverse Process는 Forward Process에서 노이즈가 추가된 데이터를 다시 원래 데이터로 복원하는 과정입니다. 이 과정은 생성된 노이즈를 거꾸로 추정하여 원래 데이터를 복원하는 방식으로 동작합니다.

수식: Reverse Process는$$p_\theta(x_{t-1}

x_t)$$로 정의되며, 이는 Forward Process의 반대 과정입니다. 이 때 각 스텝에서의 복원은 다음과 같은 가우시안 분포를 따릅니다:

[ p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t)) ]

여기서$\mu_\theta$는 학습된 모델에 의해 예측된 평균이며,$\Sigma_\theta$는 가우시안의 분산을 의미합니다. 학습 과정에서는 Forward Process에서의 노이즈를 기반으로, Reverse Process에서 어떻게 원래 데이터를 복원할지 학습합니다.

Loss Function (손실 함수)

Reverse Process에서 중요한 점은 모델이 각 스텝에서 예측하는 노이즈가 얼마나 정확한지입니다. 이때 손실 함수는 예측된 노이즈$\epsilon_\theta(x_t, t)$와 실제 노이즈$\epsilon$간의 차이를 최소화하는 방식으로 정의됩니다:

[ L_t = \mathbb{E}{x_0, \epsilon, t}\left[ |\epsilon - \epsilon\theta(x_t, t)|^2 \right] ]

이 손실 함수는 시간에 따른 노이즈 예측의 오차를 최소화하며, 모델이 점차적으로 정확하게 노이즈를 제거하는 방향으로 학습됩니다.

3. 이동 과정의 시각적 설명

위 그림에서는 각 타임스텝$T$에서 데이터가 어떻게 변해가는지 보여줍니다: -$T = 0$: 원래 데이터 분포. -$T = 1$부터$T = 8$까지: 시간이 지나면서 데이터에 노이즈가 더해지고, 데이터가 점점 퍼지며 가우시안 노이즈에 가까워집니다. -$T$가 증가할수록 데이터가 가우시안 분포를 따르며 노이즈가 많은 상태로 변합니다.

4. 모델의 역할

DDPM의 핵심 목표는 Forward Process를 통해 점진적으로 노이즈가 추가된 데이터를 보고, Reverse Process에서 그 노이즈를 제거하여 원래 데이터를 복원하는 것입니다. 학습 과정에서 모델은 점진적으로 노이즈를 제거하는 방법을 학습하며, 손실 함수는 모델이 노이즈를 얼마나 정확히 제거했는지 평가합니다.

이 방식은 노이즈가 점진적으로 더해진 데이터를 학습하여 원래 데이터를 생성하는 데 매우 강력한 방법론입니다. DDPM은 특히 이미지를 생성하는 데 탁월한 성능을 발휘하며, 다양한 생성 모델에서 사용됩니다.DDPM(Denoising Diffusion Probabilistic Models)은 생성 모델의 한 종류로, 노이즈를 점진적으로 추가한 데이터에서 원래 데이터를 복원하는 방식으로 학습 및 샘플링을 진행합니다. 이 과정은 두 단계로 나눌 수 있습니다: Forward Process와 Reverse Process. 아래에서는 수학적으로 각 과정을 설명하겠습니다.